전구_2550

문제 : 전구

문제 : 전구

간단 요약
왼쪽에는 스위치, 오른쪽에는 전구가 있고 각각 번호가 있다.
서로 일치하는 번호끼리 선이 연결되어 있을 때,
어떻게 해야 선이 교차되지 않고 가장 많이 연결할(킬) 수 있을까?
데이터
N
의미 스위치(전구) 수
범위 1 ~ 10,000
실패한 접근법
- 그리디
  전에 중량제한 포스팅과 마찬가지로,
  이번 것 역시 최대로 킬 수 있는 수와 그때의 전구 번호를 구하는 것이었기 때문에
  Greedy, DP, Binary Search가 나의 예상 범위 안에 들어왔다
  그 때 당시 팀원들과 시간을 제한하면서 풀었기에, 직관적으로 봤을 때 이 스위치와 전구의 인덱스 차이가 적으면 당연하게도 가장 많이 연결할 수 있을 줄 알았다
  다만 결론적으로 이 경우는 실패했다
  왜냐하면 아래와 같은 경우가 있기 때문이었다
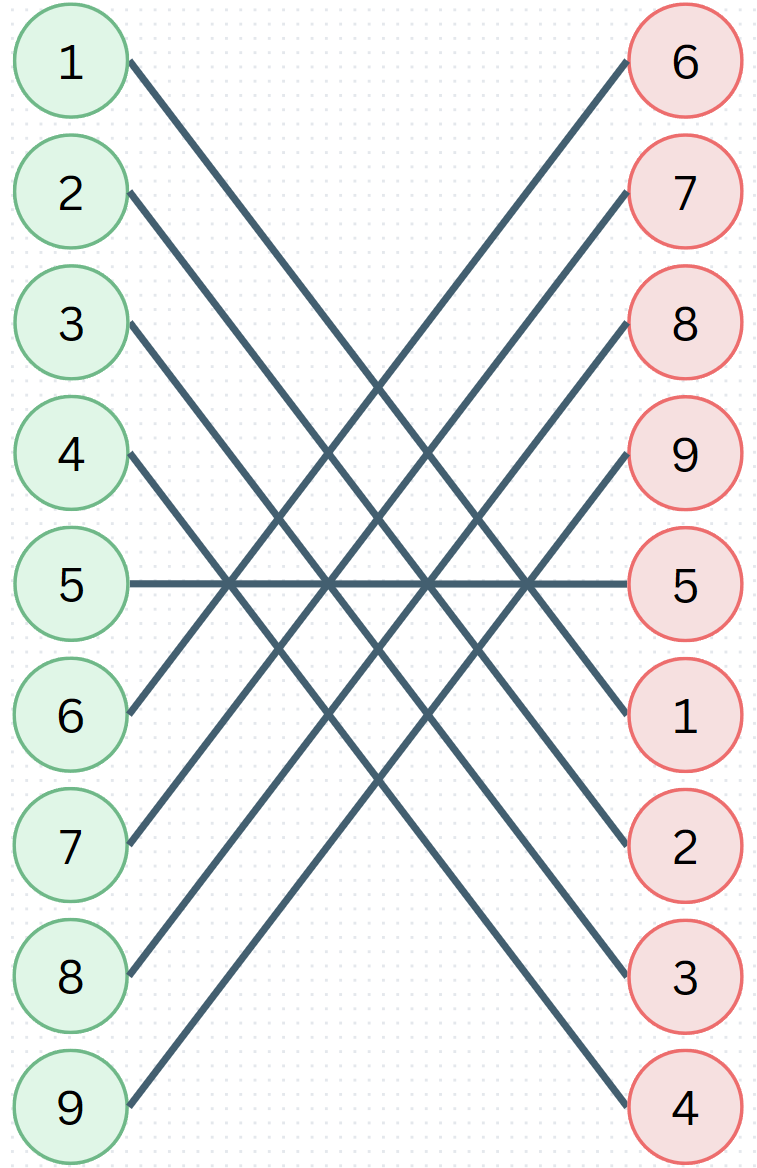
  차이가 많은 것을 우선적으로 선택할 경우 위 예시에서는 5를 먼저 선택하게 된다
  다만 이 경우 다른 것들을 선택하면 전부 꼬이므로 최대 길이가 1이라는 잘못된 답을 출력한다
접근법
이분 탐색으로 접근을 하려고 해도, 몇개를 연결할 수 있는지 테스트 하는 방법이 간단하지 않고, 그 때의 전구를 알아야 하니 불가능해보인다
결론적으로 이 문제는 LIS라는 DP 문제를 알고 있어야지 풀 수 있다
- LIS란
  Longest Increasing Subsequence
  LIS는 최장 증가 부분 수열을 말한다
  10, 50, 20, 15, 30, 40 이라는 값이 순서대로 들어왔을 때
  최장은 10, 20, 30, 40 or 10, 15, 30, 40으로 최장 길이는 4가 된다
이를 알고서 본다면, 스위치와 같은 번호의 전구가 위치한 Index를 배열로 담았을 때,
이 값들의 최장 증가 부분 수열의 길이와 그 때의 전구 번호를 출력하는 문제가 된다
위 반례 예시를 기준으로 보자면 6,7,8,9,5,1,2,3,4 가 될 것이고 이러한 값이 들어왔을 때의 최장 길이와 그 때의 전구 번호를 구하면 된다
다만 여기서 난 한가지 실수를 했다
- 잘못된 로직
```
  #include <iostream>
  #include <map>
  #include <algorithm>
  using namespace std;

  int leftLight[10001];
  int rightLight[10001];
  map<int,int> lightIdx;
  int num[10001];
  int dp[10001];


  int main(){
      ios::sync_with_stdio(false);
      cin.tie(0);

      int n;
      cin >> n;

      for(int i = 1; i <= n; i++){
          cin >> leftLight[i];
      }

      for(int i = 1; i <= n; i++){
          int data;
          cin >> data;
          rightLight[i] = data;
          lightIdx[data] = i;
      }


      for(int i = 1; i <= n; i++){
          num[i] = lightIdx[leftLight[i]];
      }

      dp[0] = 0;
      int dpSize = 0;
      int temp[10001];
      int ans[10001];
      for(int i = 1; i <= n; i++){
          int left = 0;
          int right = dpSize;
          while(left <= right){
              int mid = (left + right)/2;
              if(num[i] <= dp[mid]){
                  right = mid -1;
              }else{
                  left = mid + 1;
              }
          }
          if(left == dpSize + 1){
              dp[++dpSize] = num[i];
              for(int j = 1; j <= dpSize; j++){
              ans[j] = rightLight[dp[j]];
              }
                    
          }else{
              dp[left] = num[i];
          }
      }

      sort(ans + 1, ans + dpSize+1);
            
      cout << dpSize << "\n";   
      for(int i = 1; i <= dpSize; i++){
          cout << ans[i] << " ";
      }
  }
```
  잘못된 코드이므로 일일이 주석 설명은 생략한다.
  여기서 보면 되는 부분은 if(lfet == dpSize + 1) 쪽의 코드로,
  해당 전구가 지금까지의 전구보다도 뒤에 위치할 때 최장 길이의 숫자를 갱신했고,
  이 때 나는 그때의 dp 배열에 저장되어 있는 index를 기반으로 전구 번호를 ans에 넣고서 정렬을 돌린 뒤 출력했다
  결론적으로 이 코드는 잘못되었는데, 백준에서 제공된 기본 예시와 질문 게시판의 글의 테스트 케이스, 기타 예시를 넣어보아도
  정답이 나오는 바람에 예외를 찾기 힘들었다
  이 문제를 해결하는데 도움을 준 지인 귀인에게 너무너무 감사하다
  이 코드에서 잘못된 점은 최장 길이가 갱신될 때 dp 배열에 저장된 값이 answer라고 생각했던 점이다
  아래 예시를 보자
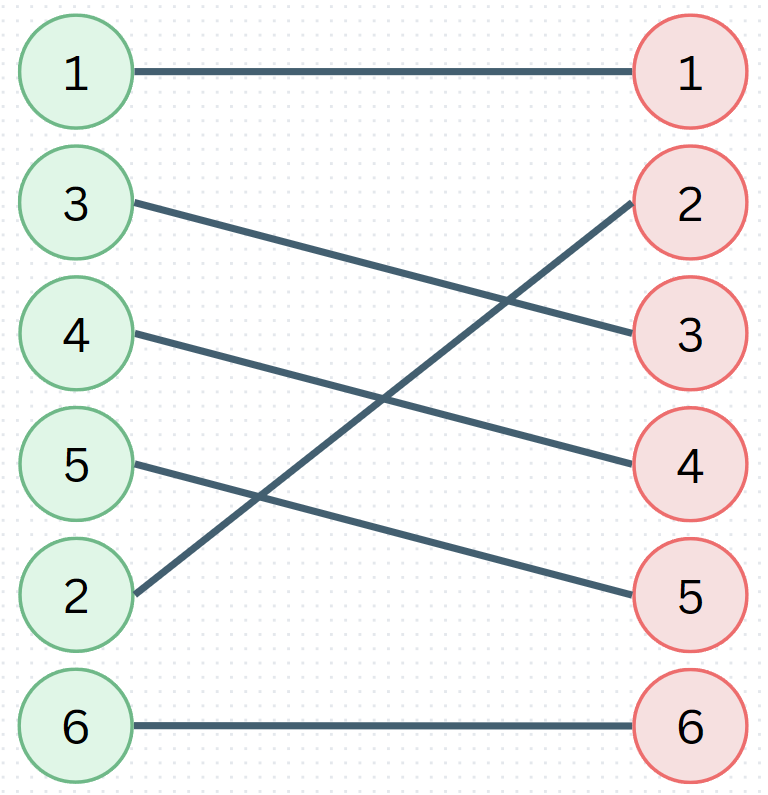
  이러한 입력이 들어올 경우 정답은 [1,3,4,5,6]이지만
  2에 대해서 진행할 때 최장배열은 3을 갈아끼워 [1,2,4,5]가 되고,
  그 다음 6이 들어오면서 [1,2,4,5,6]이 된다
  이 때 최장 길이가 늘어나게 되면서 [1,2,4,5,6]을 answer로 저장하게 되고 이를 출력한다
  - 문제점
    문제점은 2가 저곳에 위치할 수 있는 것은 맞지만, 2가 저곳에 있으면서 최장 길이가 되려면 기존의 3뿐만 아니라,
    2가 가로지른 4와 5도 모두 2보다 뒤에 있는 데이터에 의해 갈아끼워져야 했다는 것이다
    본 코드에서는 2가 3의 위치로 온 뒤에 4와 5가 바뀌지 않은채로 6이 맨 뒤로 추가되면서 더렵혀진 데이터가 answer로 등록되는 문제가 있었다
    그렇다면 어떻게 해야 할까
  - 해결책
    저장은 본 코드 그대로 진행하면서, 각 스위치마다 최장길이를 위한 전구의 최적 인덱스를 따로 저장해두었다가 뒤에서부터 탐색하면서 순서대로 전구를 찾아내는 것이다
    똑같은 위치에서 설명을 진행하면
    5번 인덱스인 2에 대해서 진행할 때 최장배열은 3을 갈아끼워 [1,2,4,5]가 되고,
    이 때 2는 2번 인덱스에 위치하므로 idxList는 [1,2,3,4,2]가 되는 것이다
    그리고 마지막 6번 인덱스의 6이 맨 뒤로 가게 되면서 idxList는 [1,2,3,4,2,5]가 된다
    그리고 뒤에서부터 탐색하면서 거꾸로 5번째부터 1번째 전구까지 찾아낸 뒤 오름차순으로 출력하기 위한 정렬을 거쳐 답을 뱉으면 된다.
    앞에서부터 탐색할 경우 앞의 데이터가 이미 뒤의 데이터에 의해서 갈아끼워졌을 확률이 있기 때문에 뒤에서부터 해야 한다

	N
의미	스위치(전구) 수
범위	1 ~ 10,000

코드

#include <iostream>
#include <map>
#include <algorithm>
#include <vector>
using namespace std;

// i번째 위치에 몇번 스위치가 들어왔는지 저장하는 배열
int leftLight[10001];
// x번 스위치와 연결된 x번 전구가 몇번째 위치에 있는지 저장하는 Map
map<int,int> lightIdx;
// 왼쪽의 i번째 위치에 있는 스위치랑 연결된 전구가 몇번째 위치에 있는지 저장하는 배열
int num[10001];
// 최장 배열을 위한 수를 기록하는 dp 배열
int dp[10001];
// i번째 스위치에 해당하는 전구가 몇번째로 켜지는 것이 좋은지 최적의 인덱스를 저장하는 배열
int numIdx[10001];

int main(){
    ios::sync_with_stdio(false);
    cin.tie(0);
  
    int n;
    cin >> n;
  
    for(int i = 1; i <= n; i++){
        cin >> leftLight[i];
    }
  
    for(int i = 1; i <= n; i++){
        int data;
        cin >> data;
        // data번 전구는 i번째에 위치한다는 것을 저장
        lightIdx[data] = i;
    }
  
  
    for(int i = 1; i <= n; i++){
      // i번째 스위치의 번호에 해당하는 전구의 위치를 구해서 num[i]에 저장
        num[i] = lightIdx[leftLight[i]];
    }
  
    dp[0] = 0;
    // 최장 길이 사이즈
    int dpSize = 0;

    for(int i = 1; i <= n; i++){
      // LIS를 찾는 방법은 O(n²)과 O(nlogn)의 방법이 있는데 이분 탐색을 통한 O(nlogn)의 방법을 채택했다
      // 이분 탐색을 통해 i번에 위치한 스위치의 전구가 몇번째로 켜지는 것이 가장 좋은지 탐색을 진행한다.
      // 위치가 높을 수록(인덱스가 낮을 수록) 뒤의 전구를 더 많이 켤 수 있을 것이기 때문에 자기가 가장 높게 올라갈 수 있는 곳을 찾는다
      // 결론적으로 left에 전구가 위치할 곳을 가리킨다.
        int left = 0;
        int right = dpSize;
        while(left <= right){
          int mid = (left + right)/2;
          if(num[i] <= dp[mid]){
              right = mid -1;
          }else{
              left = mid + 1;
          }
        }

        // 만약 left가 dpSize 즉 지금 이미 저장된 배열의 크기보다 크다면 맨 뒤로 들어간다는 것이고, 최장 길이가 늘어나는 것이므로
        if(left == dpSize + 1){
            // dpSize를 늘리면서 저장하고, 해당 전구의 최적의 인덱스를 저장한다.
            dp[++dpSize] = num[i];
            numIdx[i] = dpSize;
        }else{
            // 최장 길이가 늘어나는 것이 아니면 이미 있던 것을 바꾸면서 최적의 위치로 들어가는 것이다
            // 바꾸고서, 최적의 인덱스를 저장한다
            dp[left] = num[i];
            numIdx[i] = left;
        }
    }
    // 최장 길이를 반환하고
    cout << dpSize << "\n";
    // 거꾸로 찾아야 하므로 searchIndex를 뒤에서부터 진행한다
    int searchIdx = dpSize;
    // 최장 길이의 전구를 저장하기 위한 vector
    vector<int> v;
    // 뒤에서부터 탐색하면서 
    for(int i = n; i >= 1; i--){
        // 이미 다 찾았다면 탈출
        if(searchIdx == 0){break;}
        // 찾고자 하는 위치와 같다면
        if(searchIdx == numIdx[i]){
            // 해당 전구의 번호를 넣는다
            v.push_back(leftLight[i]);
            // 다음에 찾아야 할 번호로 세팅
            searchIdx--;
        }
    }
    // 전구 번호를 오름차순으로 출력하기 위한 sort 과정
    sort(v.begin(), v.end());
    // 정렬된 순서대로 전구 번호 출력
    for(int i =0 ; i < v.size(); i++){
        cout << v[i] << " ";
    }
}

전구_2550

문제 : 전구

간단 요약

데이터

실패한 접근법

그리디

접근법

LIS란

잘못된 로직

문제점

해결책

코드

Na2te

Error

문제 : 전구

간단 요약

데이터

실패한 접근법

그리디

접근법

LIS란

잘못된 로직

문제점

해결책

코드

Templates (for web app):

Error